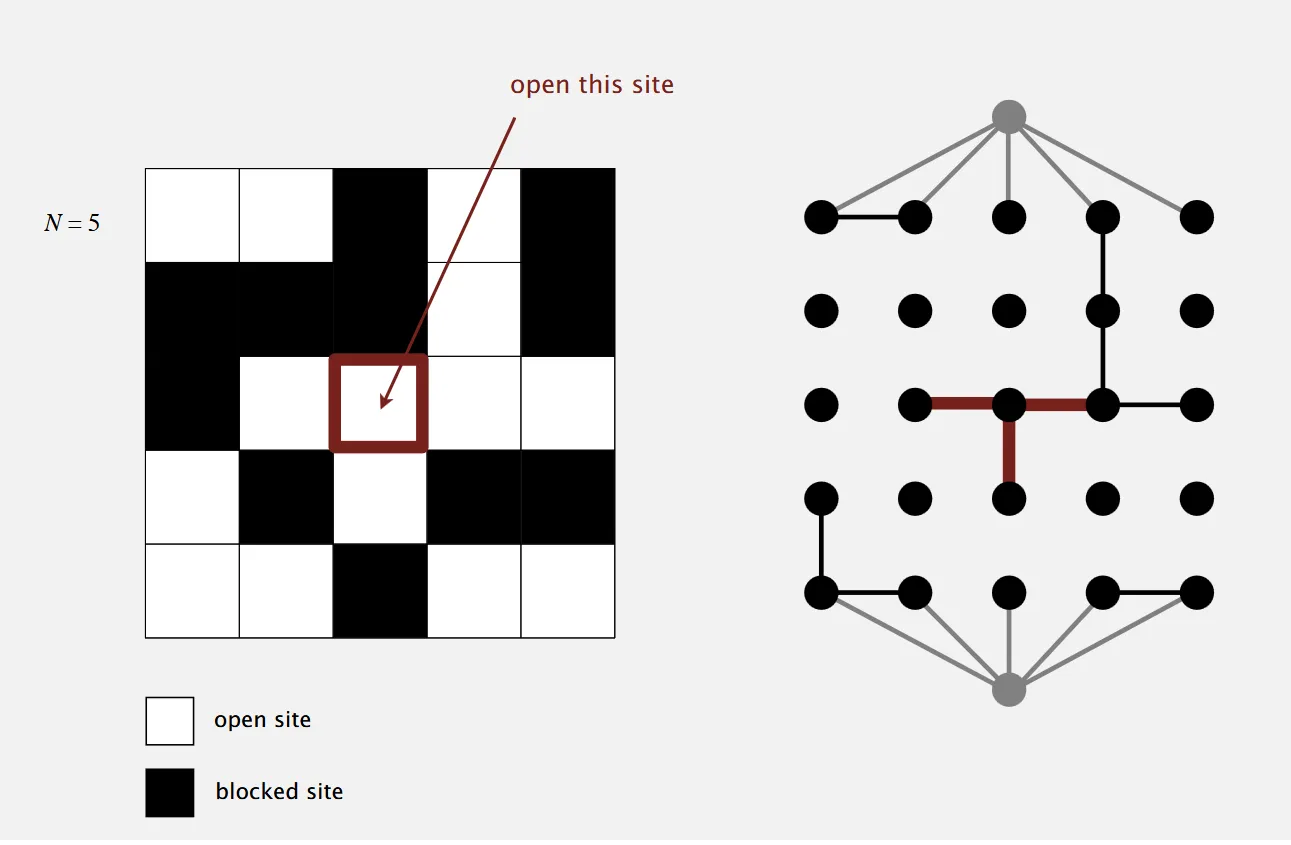
Percolation

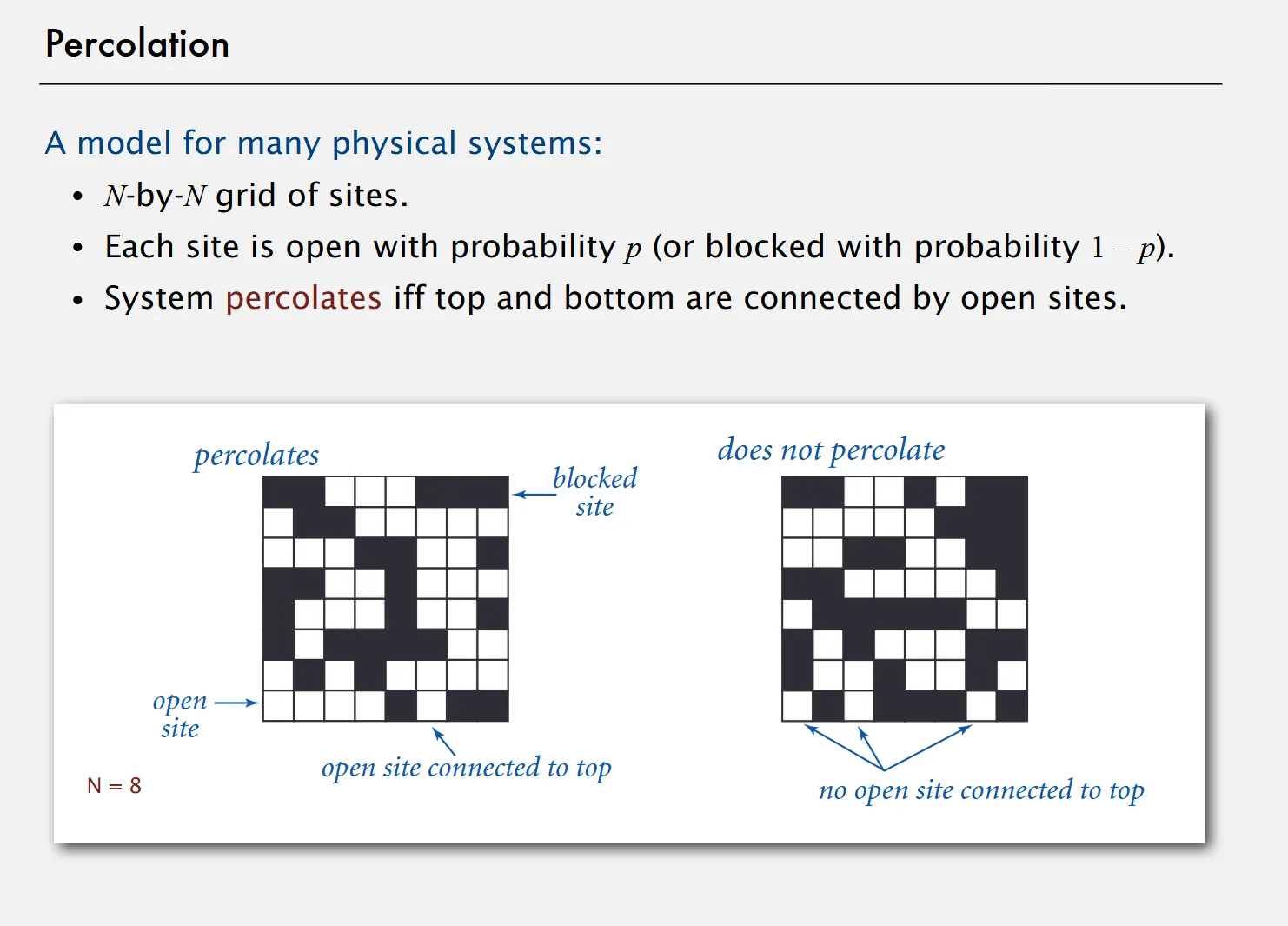
As the images demonstrate the Union-Find model can be implemented here to return if our sites percolate (connect from top to bottom).

Examples of Physical Systems

Model	System	Vacant Site	Occupied Site	Percolates
Electricity	Material	Conductor	Insulated	Conducts
Fluid Flow	Material	Empty	Blocked	Porous
Social Interactions	Population	Person	Empty	Communicates

Probability of Percolation

As percolation relies on empty sites we can determine the probability of percolation by counting 1-p or p (site is open or blocked).

Phase Transitions

A phase transition takes into account P (open site) and P * (Critical probability - the threshold at which a phase transition occurs in an infinite system.) to provide a percolation probability.

• P > P * = Almost certainly percolates
• P < P * = Almost certainly does not percolate

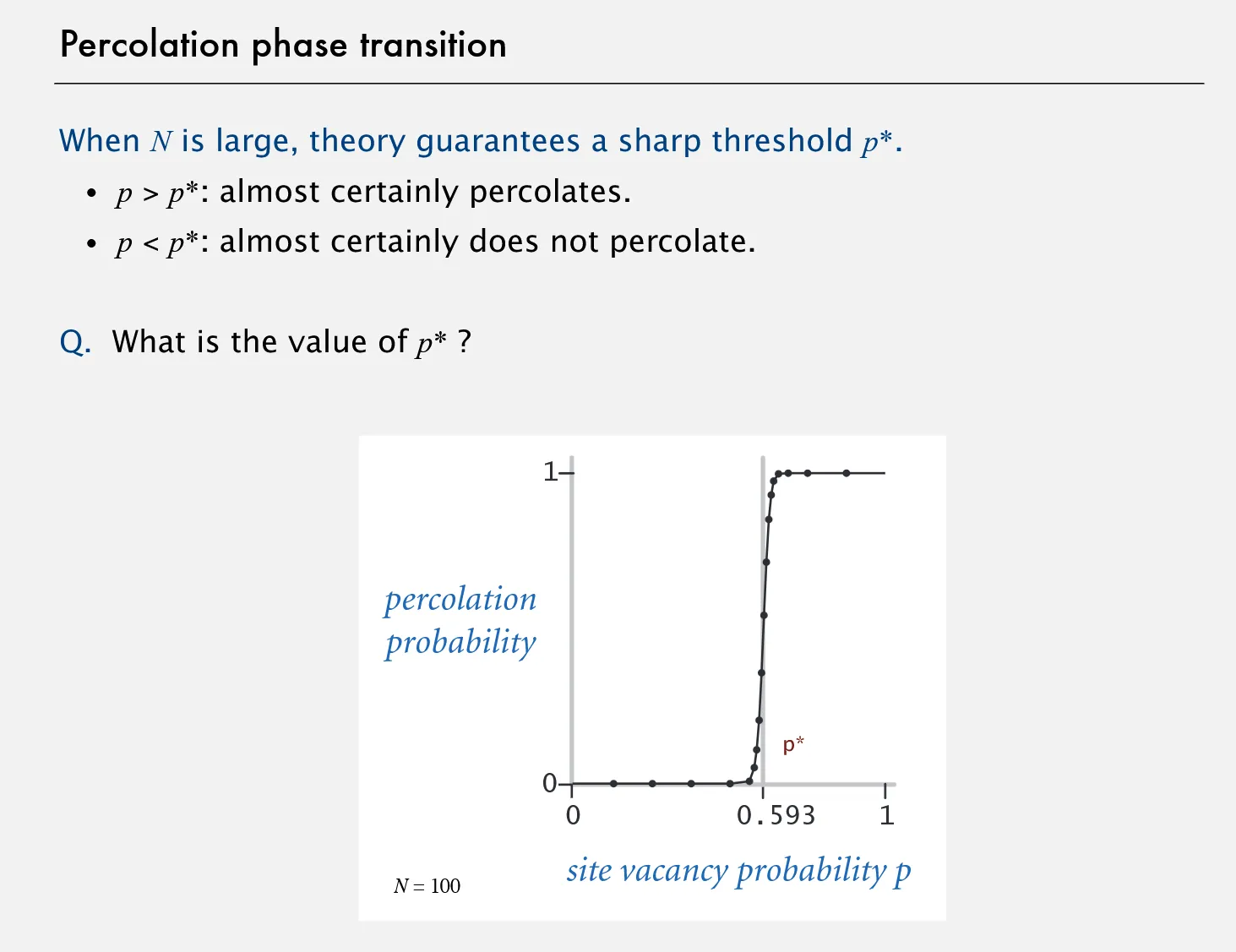
How do we calculate P *

The only solution we have to calculate the value of P * is to run a simulation to determine the value. The simulations are enabled a Fast Union Find Algorithm.

Monte Carlo Simulation

• Every time we add a random open site we check to see if the system percolates
• We keep going until the system percolates.
• The vacancy percentage at the time the system percolates is the threshold value.
• We can run the Monte Carlo Simulation multiple times to find this value on average.

How to use our Dynamic Connectivity Model to simulate.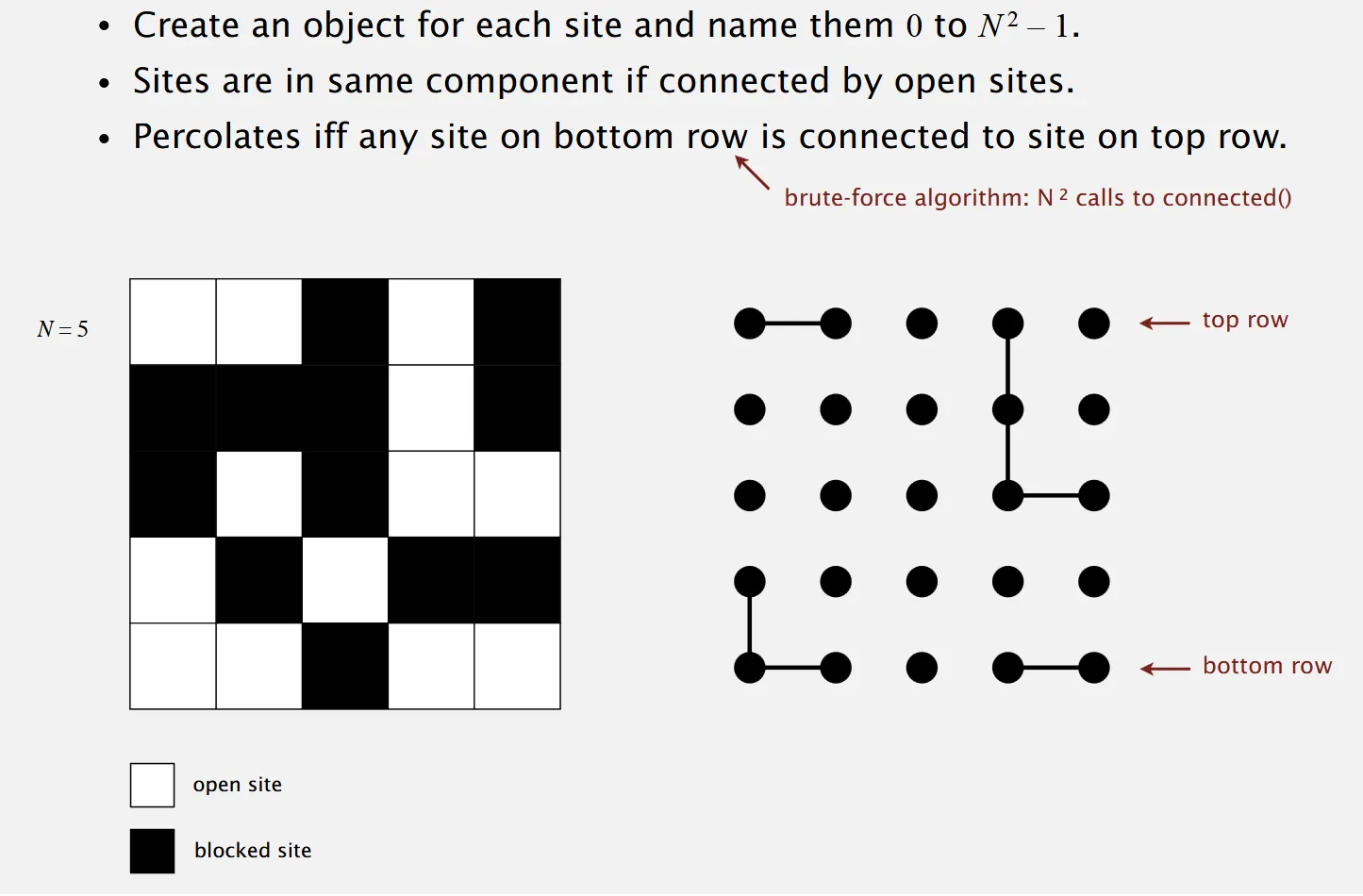

• The above image has an issue in checking if our model percolates requires a quadratic brute force to check our top row with our bottom row.
• A clever trick to implement would be to implement virtual sites on the top and bottom to run one command to check for percolation removing the requirement for a quadratic brute force algorithm as demonstrated above.

Open Sites at Random

Lastly we need to randomly open sites until our model percolates, to achieve this we select a site and mark it as open by connecting it to all of its adjacent open sites which can take up to 4 union() operations (including 0).