Weighted Quick Union

As both Quick Find and Quick Union on their own are not optimised and can cause memory heavy operations to occur we need to start improving our algorithm.

The first approach might be to apply weighting.

• We first modify the union to have bounds associated with our trees.
• Need to Keep track of our tree sizes.
• Ensure our UNION operations take into account which node is in the bigger tree and which node is in the smaller tree moving smaller trees to bigger trees.
• Should the tree sizes be equal tree’s simply merge.

A weighted quick union algorithm always ensures the smaller tree goes below.

Immediate Improvements

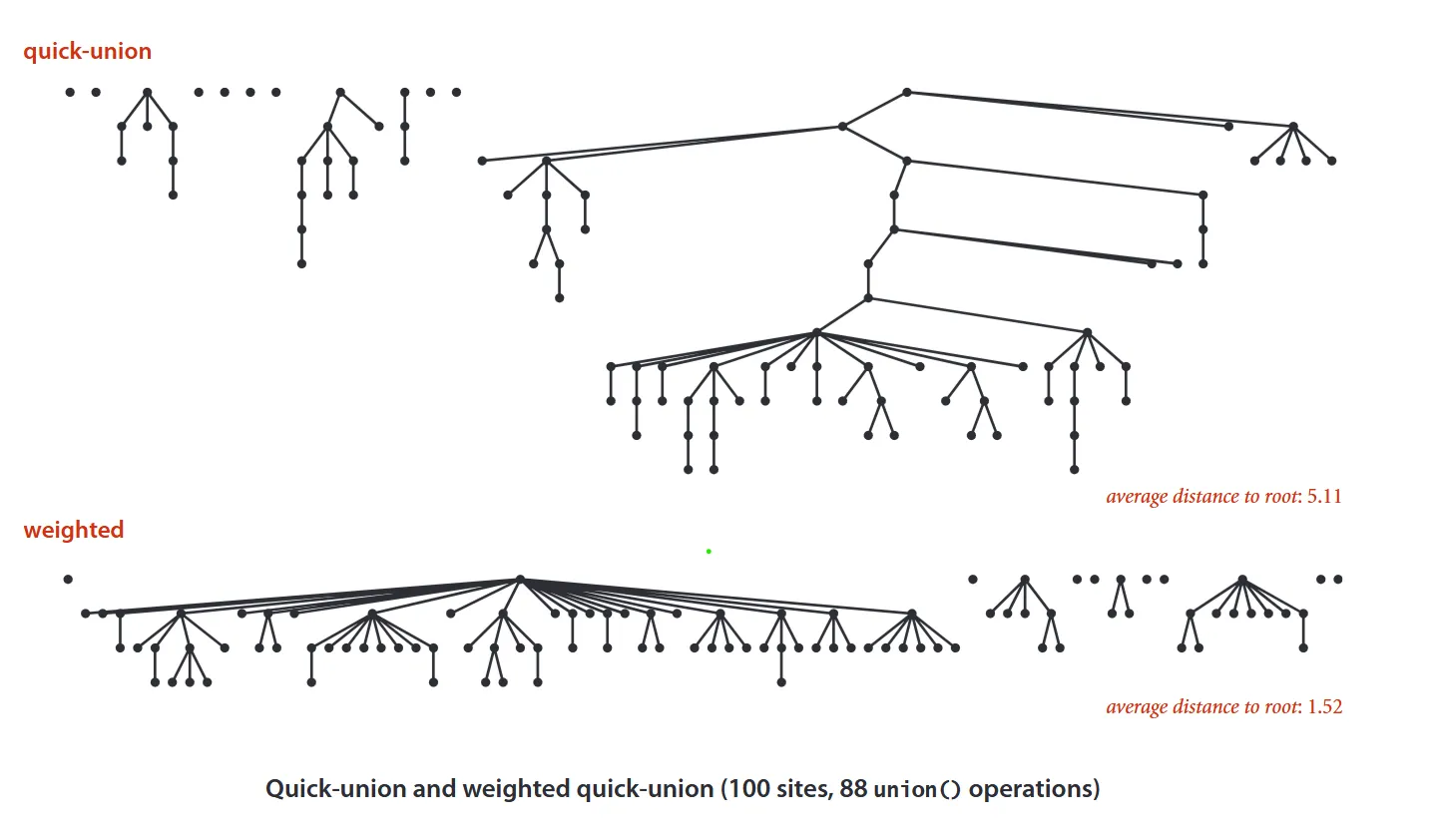
As a weighted quick union helps flatten our structure and reduces the distance between nodes we see an immediate reduction of up to on average 3x in distance between nodes resulting in significant improvements for both find and union operations.

Implementation

Data Structure

• As per our initial implementations we will us an array which takes its position as node and value as connected.
• We will also now need to take into account an extra array to count the number of objects in the tree rooted at i

  constructor(n) {
    this.id = [];
    this.sz = [];
    for (let i = 0; i < n; i++) {
      this.id[i] = i;
      this.sz[i] = i;
    }
  }

Find

• The find function remains the same using the private root class

  #root(i) {
    while (i != this.id[i]) i = this.id[i];
    return i;
  }

  connected(p, q) {
    return this.#root(p) == this.#root(q);
  }

Union

• We are going to modify the union implementation to check the sizes of each connected component linking the root of our smaller tree to the root of our larger tree.

  union(p, q) {
    const i = this.#root(p);
    const j = this.#root(q);
    if (i == j) return;
    if (this.sz[i] < this.sz[j]) {
      this.id[i] = j;
      this.sz[j] += this.sz[i];
    } else {
      this.id[j] = i;
      this.sz[i] += this.sz[j];
    }
  }
}

Updated Code In Full

// WEIGHTED QUICK UNION
class UF {
  constructor(n) {
    this.id = [];
    this.sz = [];
    for (let i = 0; i < n; i++) {
      this.id[i] = i;
      this.sz[i] = i;
    }
  }

  #root(i) {
    while (i != this.id[i]) i = this.id[i];
    return i;
  }

  connected(p, q) {
    return this.#root(p) == this.#root(q);
  }

  union(p, q) {
    const i = this.#root(p);
    const j = this.#root(q);
    if (i == j) return;
    if (this.sz[i] < this.sz[j]) {
      this.id[i] = j;
      this.sz[j] += this.sz[i];
    } else {
      this.id[j] = i;
      this.sz[i] += this.sz[j];
    }
  }
}

const test = new UF(10);
console.log(test.connected(1, 3));
test.union(1, 3);
console.log(test.connected(1, 3));

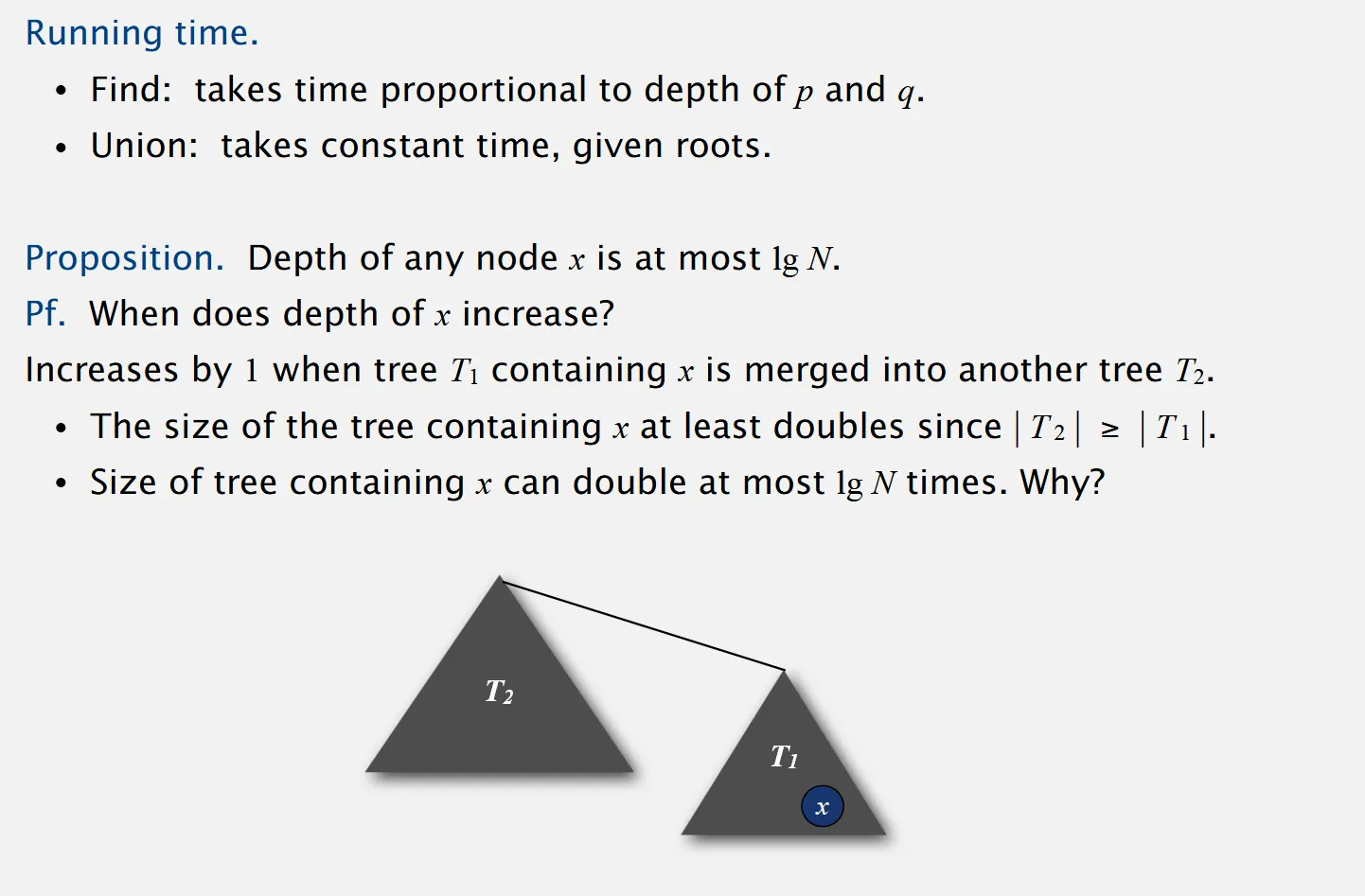
Mathematical Performance Improvements

• Find: Takes time proportianl to the depth of p and q
• Union: Takes constant time, given roots.

Depth of any node x is at most lg (Base 2 Logarithm) n

N = 1000 x = 10 N = 1000000 x = 20 N = 1B x = 30

Proof of improvement