Example - Analysis of an Algorithm (3-Sum Problem)

Given N distinct integers, how many triples sum to exactly zero?

30, -40, -20, -10, 40, 0, 10, 5

Answer: 4 (see below)

a[i]	a[j]	a[k]	sum
30	-40	10	0
30	-20	-10	0
-40	40	0	0
-10	0	10	0

Write a program that can solve this on scale efficiently.

Method 1 Brute Force (Slow - Quadratic)

//Check each triple
in N = a.length;
int count = 0;
for (int i = 0; i < N; i++ ){
  for (int j = i + 1; j < N; j++){
    for (int k = j+1; k < N; k++){
      if(a[i] + a[j] + a[k] == 0) count ++;
    }
  }
}
return count;

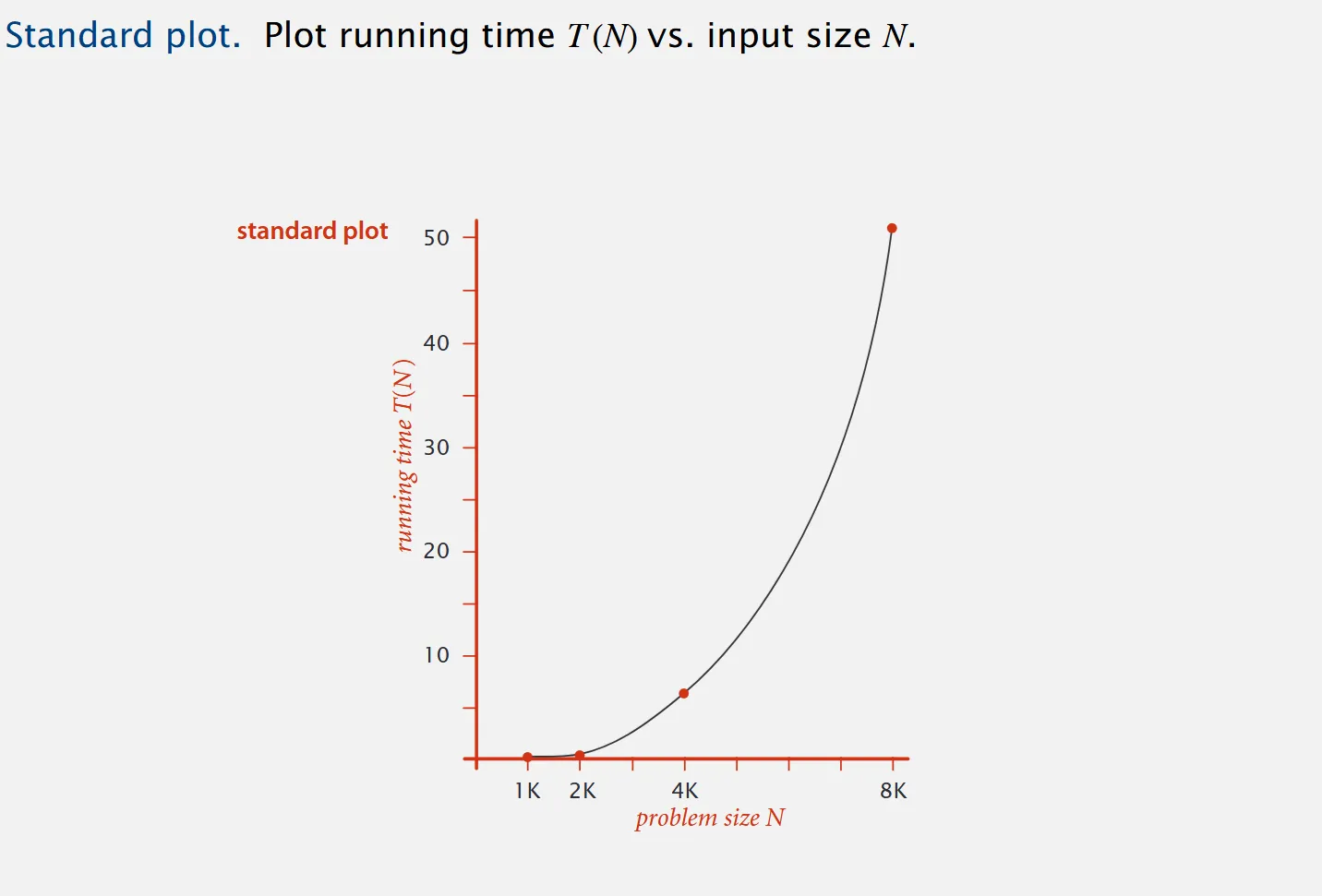
Power Law

We would first take our algorithm and plot empirical data to understand our running time and how it scales. For the above code we might get a curve as such:

N	time(s)
250	0.0
500	0.0
1000	0.1
2000	0.8
4000	6.4
8000	51.1
16000	?
Continuing from our standard plot utilising a log-log scale we can then look at the slope to understand the efficiency of our algorithm at scale:

From our hypothesis we can now predict the running time of our program

Predictions

The running time is about 1.006x 10POW(-10) x NPOW(2.999) seconds

• 51.0 seconds for N = 8,000
• 408.1 seconds for N = 16,000

Observations

N	time(seconds)
8K	51.1
8K	51.0
8K	51.1
16K	410.8
Hypothesis Validated!

Doubling Hypothesis

A quick way to estimate b in a power law relationship is by doubling our hypothesis and capturing the lg ratio.

N	Time	Ratio	lg ratio
250	0
500	0.0	4.8	2.3
1000	0.1	6.9	2.8
2000	0.8	7.7	2.9
4000	6.4	8.0	3.0
8000	51.1	8.0	3.0
Here we witness a convergence of our lg ratio to a constant of 3. Exponent of N and running time.

System Independent Effects

(Determines Exponent B in Power Law && Determines constant in a power law)

• Algorithm
• Input Data

System Dependent Effects

(Determines constant in a power law)

• Hardware
• Software
• System